Materiale didattico
Lezione del 14/10/2013
Vettori e scalari; somma di vettori, metodo grafico; i vettori e le loro componenti; vettori unitari; addizione di vettori per mezzo delle loro componenti; i vettori e le leggi della fisica; prodotto di vettori.
Lezione del 21/10/2013
La meccanica del punto materiale; il moto: principi generali; il moto rettilineo uniforme; il moto uniformemente accelerato; velocità media e velocità istantanea; il moto di caduta libera; il moto del proiettile: legge oraria e principali caratteristiche.
Lezione del 28/10/2013
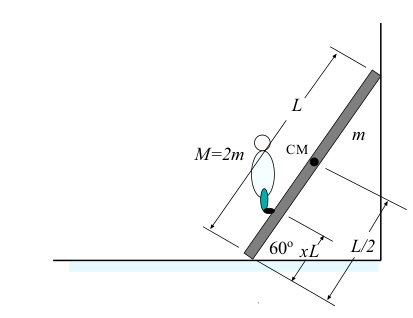
La dinamica del punto materiale: il primo principio della dinamica; sistemi di riferimento inerziali e non inerziali; il secondo principio della dinamica; il terzo principio della dinamica. Le forze: effetti statici ed effetti dinamici. La forza peso e la reazione vincolare del piano; la tensione della fune; la forza di attrito. Applicazioni: le carrucole, il piano inclinato.

 Lez. 3 - La dinamica del punto materiale (pptx) - 6.59 MB
Lez. 3 - La dinamica del punto materiale (pptx) - 6.59 MB
 Dinamica del punto materiale - appunti (pdf) - 910.22 kB
Dinamica del punto materiale - appunti (pdf) - 910.22 kB
Lezione del 04/11/2013
La meccanica del moto circolare: legge oraria, grandezze lineari e grandezze angolari; il moto periodico; la forza centrifuga; l’automobile in curva piana; l’automobile in curva rialzata; la legge di gravitazione universale; le leggi di Keplero; la velocità di fuga; i satelliti geostazionari

 Lez. 4 - La meccanica del moto circolare (pptx) - 5.59 MB
Lez. 4 - La meccanica del moto circolare (pptx) - 5.59 MB
 Cinematica e dinamica del moto circolare (pdf) - 897.6 kB
Cinematica e dinamica del moto circolare (pdf) - 897.6 kB
Lezione del 11/11/2013
Lavoro ed energia: il lavoro di una forza costante, il lavoro di una forza non costante; l’energia cinetica; l’energia potenziale; la forza elastica, la legge di Hooke; l’energia elastica; il teorema dell’energia cinetica; il teorema di conservazione dell’energia meccanica; forze conservative e non conservative; il lavoro della forza di attrito
Lezione del 18/11/2013
Esercizi sul teorema di conservazione dell’energia. Complementi di dinamica: la quantità di moto e la sua conservazione; l’impulso di una forza; il teorema dell’impulso; il momento di una forza; il teorema del momento angolare; problemi d’urto: urti elastici e completamente anelastici; il pendolo balistico. La dinamica dei sistemi di punti materiali: il centro di massa; teorema del centro di massa

 Lavoro ed energia 2 (pptx) - 5.95 MB
Lavoro ed energia 2 (pptx) - 5.95 MB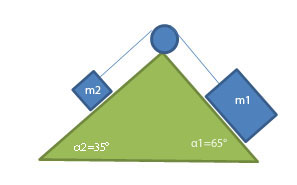
 Lez. 6 - Dinamica dei sistemi materiali (pdf) - 922.09 kB
Lez. 6 - Dinamica dei sistemi materiali (pdf) - 922.09 kB
 Lezione 06 - Complementi di dinamica (pptx) - 2.34 MB
Lezione 06 - Complementi di dinamica (pptx) - 2.34 MB
Per gli aspetti teorici relativi agli argomenti trattati in data odierna fare riferimento al testo Mencuccini – Silvestrini pp.104-107, pp. 211-228, pp. 312-319
Lezione del 28/11/2013
L’energia cinetica di un sistema di punti materiali;equazioni cardinali della dinamica dei sistemi; centro di massa di sistemi continui; il teorema di Koenig. I sistemi rigidi: il moto rotatorio; il momento torcente; dinamica rotazionale e inerzia; il momento d’inerzia; momento d’inerzia di sistemi continui; energia cinetica di un corpo rigido; sfera che rotola lungo un piano inclinato; la macchina di Atwood reale; il lavoro del momento torcente; il momento angolare e la sua conservazione.
Lezione del 02/12/2013
Gli atomi e la materia; la teoria atomica; il moto browniano; i sistemi termodinamici; la temperatura; i termometri; la dilatazione termica; gli sforzi termici; stati di equilibrio termodinamico; la legge fondamentale della termologia; il calore; il calore e i passaggi di stato; il calore latente; la propagazione del calore: legge di Fourier, legge di Stefan-Boltzmann; il calorimetro; le trasformazioni termodinamiche; i gas e la temperatura; l’equazione di stato dei gas; le leggi dei gas; il lavoro in termodinamica; l’esperimento di Joule; l’equivalente termico della caloria.
Lezione del 06/12/2013
Il I principio della termodinamica; le trasformazioni dei gas: isocora, isobara e isoterma e loro rappresentazione nel piano di Clapeyron; la trasformazione adiabatica; calori specifici di un gas perfetto e relazione di Mayer; i gas reali e l’equazione di Van der Walls; i cicli termodinamici; le macchine termiche; il secondo principio della termodinamica; il ciclo di Carnot; il teorema di Carnot
Lezione del 09/12/2013
Applicazioni numeriche. Interventi di coaching e scaffolding didattico



 Facebook
Facebook Email
Email RSS
RSS